Fracciones

SUMA DE FRACCIONES

Sumar fracciones es un procedimiento bastante sencillo. Sin embargo, suelen aparecer inquietudes cuando ambas fracciones tienen denominadores diferentes. Aprende cómo resolver la suma de fracciones con diferente e igual denominador a través de la siguiente información.

Paso 1: asegúrate de que los números de abajo (los denominadores) son iguales

Paso 2: suma los números de arriba (los numeradores). Pon la respuesta sobre el denominador del paso 1

Paso 3: simplifica la fracción (si hace falta)

Ejemplo 1:

1	+	1
4		4

Paso 1. Los números de abajo son los mismos. Ve directamente al paso 2.

Paso 2. Suma los números de arriba y pon la respuesta sobre el denominador:

1	+	1	=	1 + 1	=	2
4		4		4		4

Paso 3. Simplifica la fracción:

Ejemplo 2:

Paso 1: Los números de abajo son diferentes. Así que necesitamos hacerlos iguales.

Podemos multiplicar arriba y abajo de 1/3 por 2 así:

1	=	2
3		6

y ahora los números de abajo (los denominadores) son iguales, nuestro problema queda así:

2	+	1
6		6

Paso 2: Suma los números de arriba y ponlos sobre el mismo denominador:

2	+	1	=	2 + 1	=	3
6		6		6		6

Paso 3: Simplifica la fracción:

3	=	1
6		2

RESTA DE FRACCIONES

Restar fracciones es un procedimiento bastante sencillo. Sin embargo, suelen aparecer inquietudes cuando ambas fracciones tienen denominadores diferentes. Aprende cómo resolver la resta de fracciones con diferente e igual denominador a través de la siguiente información.

Paso 1: Asegúrate de que los números de abajo (los denominadores) sean iguales

Paso 2: Resta los números de arriba (los numeradores). Pon la respuesta sobre el denominador del paso 1

Paso 3: Simplifica la fracción (si hace falta)

Ejemplo 1:

3	-	1
4		4

Paso 1. Los números de abajo son los mismos. Ve directamente al paso 2.

Paso 2. Resta los números de arriba y pon la respuesta sobre el denominador:

3	-	1	=	3 - 1	=	2
4		4		4		4

Paso 3. Simplifica la fracción:

2	=	1
4		2

Ejemplo 2:

1	–	1
2		10

Paso 1: Los números de abajo son diferentes. Así que necesitamos hacerlos iguales.

Podemos multiplicar arriba y abajo de 1/2 por 5 así:

1	=	5
2		10

Y ahora los números de abajo (los denominadores) son iguales, nuestro problema queda así:

5	-	1
10		10

Paso 2: Resta los números de arriba y ponlos sobre el mismo denominador:

5	-	1	=	5 - 1	=	4
10		10		10		10

Paso 3: Simplifica la fracción:

4	=	2
10		5

MULTIPLICACIÓN DE FRACCIONES

Para multiplicar fracciones:

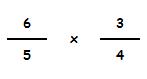
Se multiplican sus numeradores y sus denominadores:

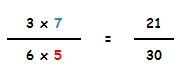
Vamos a ver otros ejemplos:

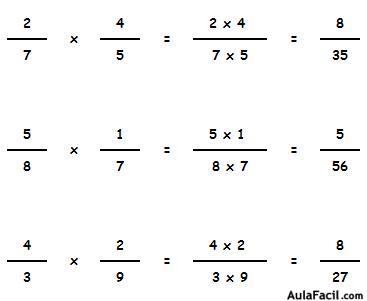
DIVISIÓN DE FRACCIONES

Cuando se dividen 2 fracciones:

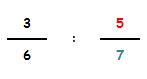
La fracción resultante tendrá:

Como numerador: el resultado de multiplicar el numerador de la primera por el denominador de la segunda.

Como denominador: el resultado de multiplicar el denominador de la primera por el numerador de la segunda.

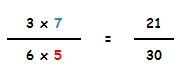
Vamos a ver otros ejemplos:

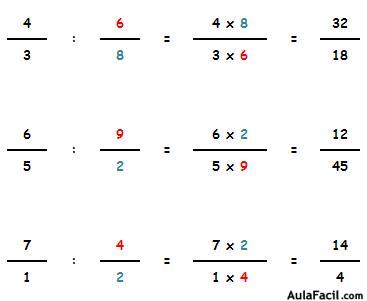
De manera simplificada:

14	=	7
4		2